How To Find The Area Of A Circle: A Quick And Simple Guide
Circles, fundamental geometrical shapes, have captivated mathematicians and scientists for over a millennium. Our understanding of the properties of circles has proved crucial to understanding orbits, launching satellites into space, designing and constructing objects with curvature, and much more. This article will guide you on how to find the area of any circle easily.

The Circle and its dimensions
A circle is a two-dimensional shape characterized by its single curved boundary. A circle can be described as the path made by joining points equidistant from a point known as its center.
Some dimensions that can be used to define a circle are:
Radius: The distance of all points in the path to the center is constant, and is known as the radius.
Circumference: The boundary/ perimeter of the circle is known as its circumference.
Diameter: The line segment through the center connecting two distinct points on the circumference. The diameter is twice the length of the radius.
Area of a Circle
The area is a property that describes the amount of space occupied by a 2d shape. The formula that is used to calculate the area of a circle is:
Area of a Circle = π r2
Where r is the radius of the circle.

Another variant of the formula can be derived by replacing the radius r, in terms of the diameter. Since the radius r is half of the Diameter, we can replace “r” by “D/2”.
Area of a Circle = π (D/2)²
Simplifying this, we get:
Area of a Circle = (π D²/4)
Depending on whether you know the radius or diameter of a circle, you apply one of the variants of the formulas above to find the area of the circle.
Example Of Finding Area Of A Circle
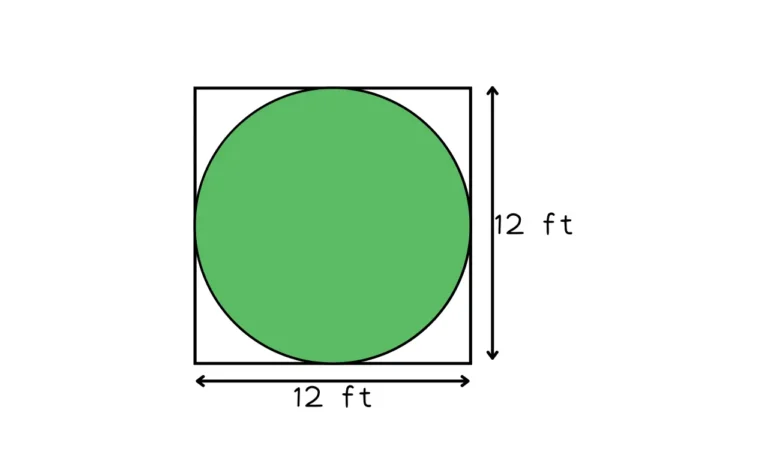
Question: What is the area of the largest circular carpet that can fit inside a 12×12 ft room?
Solution:
Step 1 : Sketch a diagram and label the information
Step 2: Determine the radius of the circle
The diameter of the largest circle that fits the square will be 12 ft. This means the circle will have a radius of 6 ft.
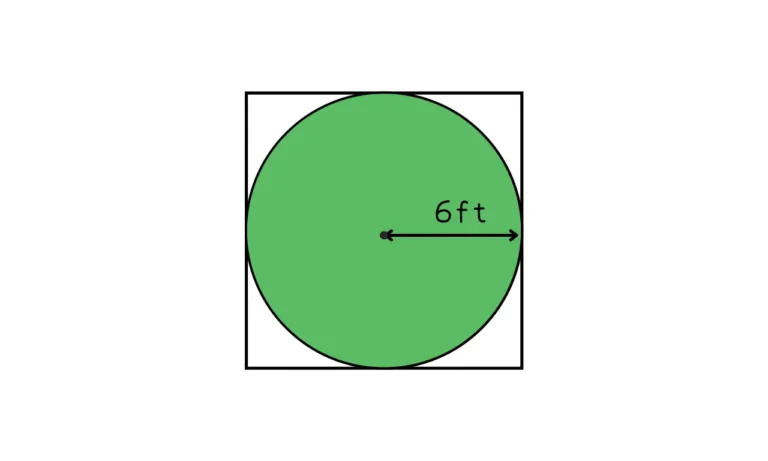
Step 3: Apply the formula for the area
Area of circle = π r2
Area of Circle = π × 6²
Area of Circle = 36 π
Step 4: Simplify
You can either leave the answer in terms of π, or simplify by substituting the value of pi.
Area of Circle = 113.10 ft2 (rounded to 2 d.p.)
Area of Sectors
Sectors are parts of circles. You can think of a sector as a slice of a circle. A sector is bound by two radii and an arc. We can utilize the formula for the area of a whole circle to obtain the area of sectors.
When finding the area of a sector we need to find out what fraction of the circle the sector is. For example, consider a semi-circle. We know that a semi-circle is half of a circle, hence its area is half that of a full circle.
For other sectors, it may not be easy to determine the portion out of the whole circle just by inspection. Here, we can utilize the central angle of the sector. For example, if we have a sector with a central angle of 40 degrees. We can calculate the fraction considering that a circle has a total angle of 360 degrees.
Fraction of Sector out of the whole circle = 40/360 = 1/9
Using this fraction, we calculate the sector’s area by multiplying the fraction by the area of the whole circle.
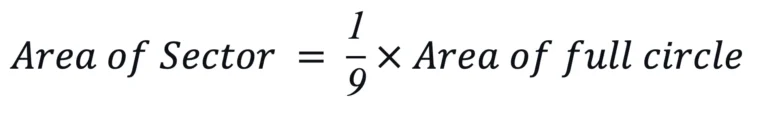
Another Example Of Finding Area Of A Circle
Question: Find the area of a sector with a radius of 5 inches and central angle of 120o

Solution:
Step 1 : Obtain the fraction of the sector
Fraction of Sector out of the whole circle = 150/360 = 5/12
Step 2: Apply the formula for the area
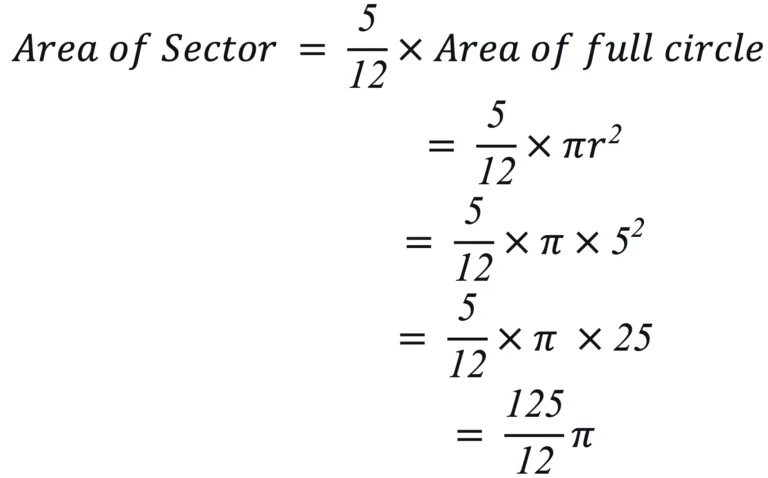
Step 3: Simplify
You can either leave the answer in terms of π, or simplify by substituting the value of pi.
Area of Sector = 32.72 in2 (rounded to 2 d.p.)
Conclusion
Understanding how to calculate the area of a circle and its sectors not only enriches your mathematical skills but also applies to practical situations. Whether you’re planning a garden layout, designing a circular pool, or simply helping with homework, these calculations are invaluable tools.