How To Use The Pythagorean Theorem To Find Missing Side Lengths

The Pythagorean Theorem stands as one of the most renowned theorems in mathematics, especially vital when studying triangles. This article aims to guide you through the various applications of the Pythagorean theorem, empowering you to confidently tackle problems.

The Pythagorean Theorem

This theorem elucidates a fundamental relationship between the lengths of three sides of a right triangle. It’s important to note that the Pythagorean theorem exclusively applies to right triangles.

Key features of a right triangle include:

One interior angle measures 90 degrees, constituting a right angle.
The longest side, known as the hypotenuse, always lies opposite the right angle.

The theorem states that the square of the length of the hypotenuse in a right triangle equals the sum of the squares of the other two legs:

c² = a² + b²

Here, c represents the hypotenuse, while a and b denote the other two sides, with their labels interchangeable.

How to recognize a right triangle

Before applying the Pythagorean theorem, it’s crucial to confirm that the triangle in question is indeed a right triangle. The presence of a right angle, often represented using a square symbol, serves as the most straightforward indication.

Alternatively, you can determine a right triangle based on:

Perpendicular sides: If two sides are perpendicular, such as one being vertical and the other horizontal, it confirms the presence of a right angle. Similarly, directional indicators like North and East/West can signify perpendicularity.
Theorems concerning triangle elements: For instance, if one side is a tangent and the other is a radius, the inherent properties of tangents validate the existence of a right angle.
Shape properties: Shapes like squares and rectangles inherently possess right angles, making it essential to consider such details.

How To Find Missing Side Lengths

The most straightforward use case of the Pythagorean theorem is to determine missing side lengths in a right triangle. Let’s look at one such example:

Example #1:

Find the missing side of the following right triangle.

The side which is missing the length is the longest side (hypotenuse).

Step 1: Label the sides, a, b, and c.

We label the right triangle just for the convenience when applying the Pythagorean theorem. Here “c” is always the hypotenuse, and a, and b can be interchanged.

Let a = 5 in and b = 12 in

Step 2: Substitute the known and unknown values into the Pythagorean Theorem

c² = a² + b²

c² = 5² + 12²

Step 3: Simplify and solve for c

c² = 25 + 144

c² = 169

c = √ 169

c = 13

Hence, the missing side length is 13 inches.

Let’s now look at an example that involves a real-life context.

Real-Life Missing Side Length Question

Mike is using a ladder to paint a mural on a high vertical wall. He positions the ladder 1.5 meters away from the base of the wall. If the ladder extends 5 meters, what is the maximum height of the wall that Mike can reach?

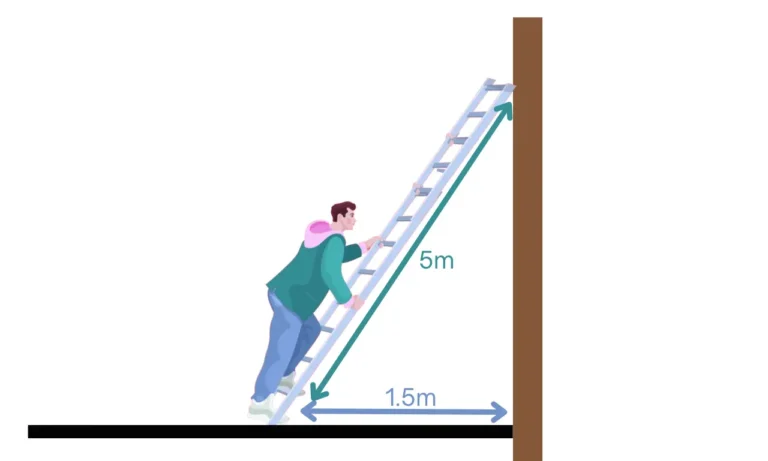
Step 1: Verify the right triangle.

The angle between the vertical wall and the floor makes a right angle, thus the ladder, wall, and floor make up three sides of a right triangle.

Step 2: Identify the sides

We can use the Pythagorean theorem to find the maximum height Mike can reach. The theorem states that in a right triangle, the square of the length of the hypotenuse (the ladder, in this case) is equal to the sum of the squares of the lengths of the other two sides (the distance from the base of the wall to the ladder, and the height Mike can reach).

Step 3: Apply the Pythagorean theorem

c² = a² + b²

Where:

c is the length of the ladder = 5 meters

a is the distance from the base of the wall to the ladder = 1.5 meters

b is the maximum height Mike can reach (what we’re trying to find)

Step 4: Substitute and solve for b

5² = 1.5² + b²

b² = 5² – 1.5²

b² = 25 – 2.25

b² = 22.75

b = √ 22.75