Introduction to 3D Shapes: Cubes, Spheres, and Cylinders
Let’s dive into the intriguing world of shapes! Shapes are everywhere, from the cylindrical soda cans to the spherical shape of the Earth. In this article, let’s explore three popular 3D shapes: cubes, spheres, and cylinders.

What are 3D Shapes?
Unlike flat, two-dimensional shapes like circles and squares, 3D shapes have depth in addition to width and height, which allows us to measure their volume. The most common 3D shapes include cubes, spheres, and cylinders, each with unique properties and uses.
Cube
What do dice, Rubik’s cubes, and sugar cubes have in common? They are all in the shape of a cube! A cube is like a square but with an added dimension. It has six faces, all square in shape, twelve edges, and eight vertices where the edges meet.
Properties of a cube
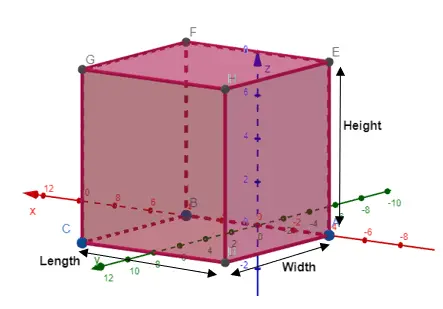

As a 3D structure, you can measure a cube’s surface area and volume. The area of the shape’s face/s is the surface area, while the volume measures how much space the shape occupies.
For a cube volume = Length x Width x Height.
Cubes are interesting because they have equal length, width, and height, which we’ll refer to as ‘a’. The volume of a cube can be calculated as:
Volume of Cube = a3
Furthermore, since the cube has six faces, the total surface area is six times the area:
Surface Area of Cube = 6 x a2
Cross-Section
A cross-section is the shape that results from cutting through a 3D object with a plane. This cut reveals the intersection of the object with the plane and provides valuable insight into the object’s internal structure, symmetry, and properties. By examining cross-sections, we can better understand the spatial dimensions and characteristics of 3D objects.
A cube exhibits uniform cross-sections when cut along planes parallel to its faces. In this scenario, each cross-section will be a square, maintaining a consistent shape and size throughout.
Sphere
Consider the planets and your favorite sports balls — they are all spheres. A sphere is a perfectly round 3D object that doesn’t have edges or vertices. Its symmetry means it looks the same from any angle, a property called isotropy.
Surface Area and Volume
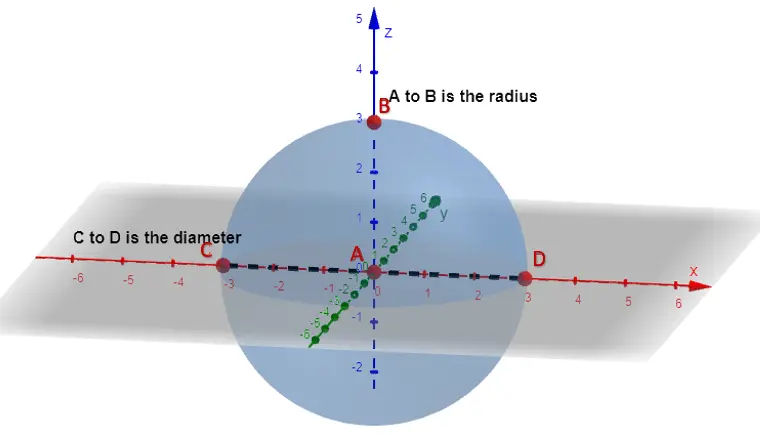
The dimensions that are used to define a sphere are its radius and diameter (labeled in the diagram above).
Like the circle, the formula for measuring the diameter (D) is twice the length of the radius (r).
Surface area of a Sphere = 4π r2
The formula for volume a sphere = 4/3(π r3).
Another property of the sphere is that it has a non-uniform cross-section. When sliced along an axis passing through its center, the resulting cross-section forms a circle. As you slice further away from the center, the cross-section progressively diminishes in size, illustrating its non-uniform nature.
Cylinder
Cylinders are common in everyday objects like cans and pillars. They are formed by two circular bases connected by a curved surface. If you imagine a pencil without the pointed ends, you’re thinking of a cylinder.
Properties of a cylinder
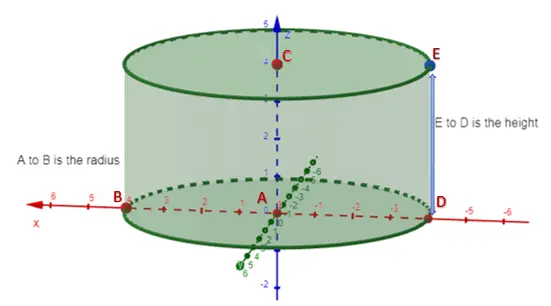
The total surface area of a cylinder consists of two identical flat circular faces and one curved face. To find the total surface area, we calculate the areas of the curved and flat surfaces separately and then add them together.
To determine the area of the curved surface, we can use the net of the cylinder.

This net shows that the curved surface unfolds into a rectangle. The length of this rectangle is the circumference of the base (2πr), and its width is equal to the height of the cylinder.
The formulas for surface area can derived as follows:
Curved Surface Area = 2π rh
Area of each Flat Circular base = π r2
Total surface area = 2π rh + 2π r2
The volume is the product of pi multiplied by the radius squared into the height. V= π r2h
Conclusion
In summary, 3D shapes play a vital role in shaping the world around us, whether it’s building structures/products or understanding nature. This is why the formulas to calculate volume and surface areas are so important, to calculate how much space these 3D structures can occupy. This can in turn develop your knowledge and perception of the object around you.