A Simple Introduction To Polar Coordinates
Coordinate systems play a vital role in various practical applications such as navigation, robotics, and mapping. This article aims to introduce you to an alternative coordinate system known as polar coordinates and explore its functionality.

Why do we need a coordinate system?
The primary purpose of a coordinate system is to provide a consistent method for defining points in space relative to a reference point. In the Cartesian coordinate system, points are defined based on their horizontal and vertical distances from the origin. For instance, on a Cartesian plane, the coordinate (2, 5) indicates a point located 2 units to the right and 5 units vertically upwards from the origin (0, 0).

Once we establish this fundamental geometric element—the point—we can use the same coordinate system to represent other objects such as lines, circles, curves, vectors, and more.
The Cartesian system employs the sign of the values to denote direction, where a positive x-coordinate indicates movement to the right, while a negative x-coordinate implies movement to the left. Similarly, a positive y-coordinate signifies movement upwards, while a negative y-coordinate indicates movement downwards.
The examples above illustrate the workings of the 2D Cartesian plane. This coordinate system can seamlessly extend to higher dimensions by incorporating additional axes. For instance, the 3D coordinate system employs three values (x, y, z) to define coordinates.
While the Cartesian coordinate system is renowned for its simplicity, it may encounter limitations when representing complex curves and specific applications. In such cases, the polar coordinate system emerges as a preferred alternative.
Polar Coordinate System
The polar coordinate system offers an intuitive approach to describing point locations within a grid. Consider the point P on the grid below. Initially, we might denote its location by its distance from the origin, which we’ll label as “r”. However, as depicted in the figure on the right, there could be infinitely many points equidistant from the origin, forming a circumference around it.
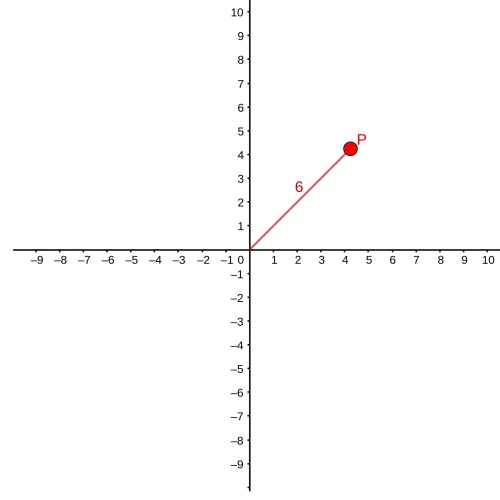
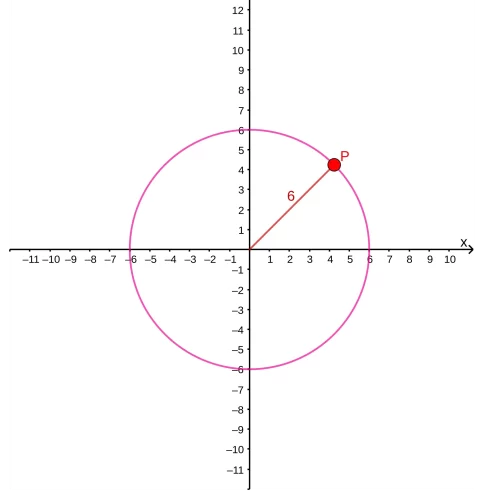
To provide additional clarity and distinguish point P from others, the polar coordinate system introduces another parameter: the angle formed with the x-axis.
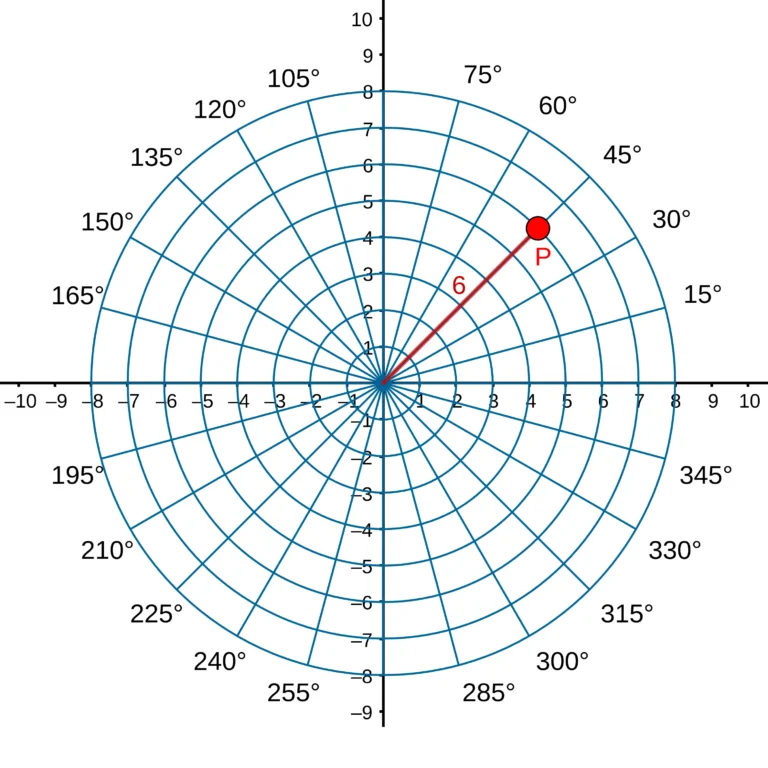
As shown in the diagram above, a polar coordinate system uniquely identifies P using the values 6 and 45o.
In this system, we define the location of point P as (r, θ), where “r” represents the distance from the origin, and “θ” denotes the angle made by the line segment (OP) with the x-axis. Following convention, this angle is measured in radians and proceeds in a counterclockwise direction from the x-axis.
Angle measure in radians
Radian measure provides an alternative way to quantify angles, particularly in trigonometry and calculus. Unlike degrees, which divide a circle into 360 equal parts, radians are based on the ratio of the arc length to the radius of the circle. In this system, one radian corresponds to the angle subtended at the center of a circle by an arc whose length equals the radius.

Consequently, a full circle encompasses 2π radians, as its circumference is 2π times its radius. To convert from degrees to radians, one can use the formula:

For example, 90 degrees would be:
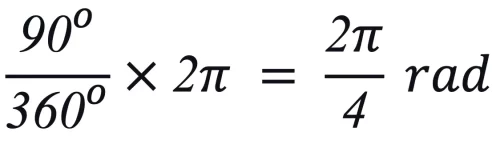
When simplified, 90 degrees is π/2 radians.
Example #1
What are the polar coordinates of the point located in the opposite direction of P, but at an equal distance from the center?
Step 1: We can start off by marking P1 point on the grid.

Step 2: Determine the distance from the origin (r) and the angle it makes with the x-axis.
The length of OP1 is 6 units, and the angle in the counterclockwise direction between the x-axis and the line segment is 225 degrees.
We need to convert 225o into radians.
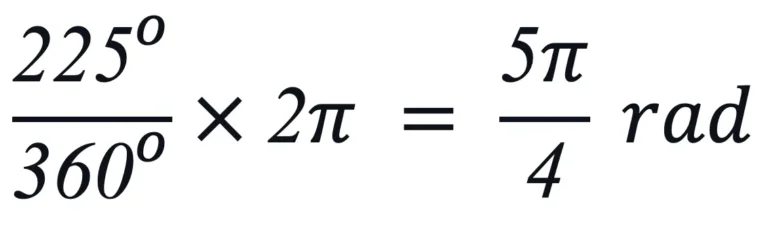
Step 3: Write the polar coordinates of the point (r,θ)
The polar coordinates of P1 are (6, 5π/4).