What Are Circle Theorems In Geometry?
Circle theorems are fundamental principles in geometry that unlock the mysteries of circular shapes. They help us understand angles, segments, and relationships within circles, guiding us in solving geometric problems. In this article, we’ll delve into the basics of circle theorems.

Defining a Circle
Before we dive into circle theorems, let’s grasp the essence of what a circle truly is. A circle is a perfectly round shape defined by all points equidistant from a central point. Simply put, a circle is a perfectly round two-dimensional shape.
In understanding circles, it’s crucial to remember a few key elements: the radius, which measures the distance from the center to any point on the circle’s edge; the diameter, which is simply twice the length of the radius; and lastly, the circumference, which refers to the total length around the circle’s perimeter.
Overview of Circle Theorems
Circle theorems are fundamental to calculating missing angles and lengths within the circle. However, before we get started you must have an understanding of the basic elements related to a circle.
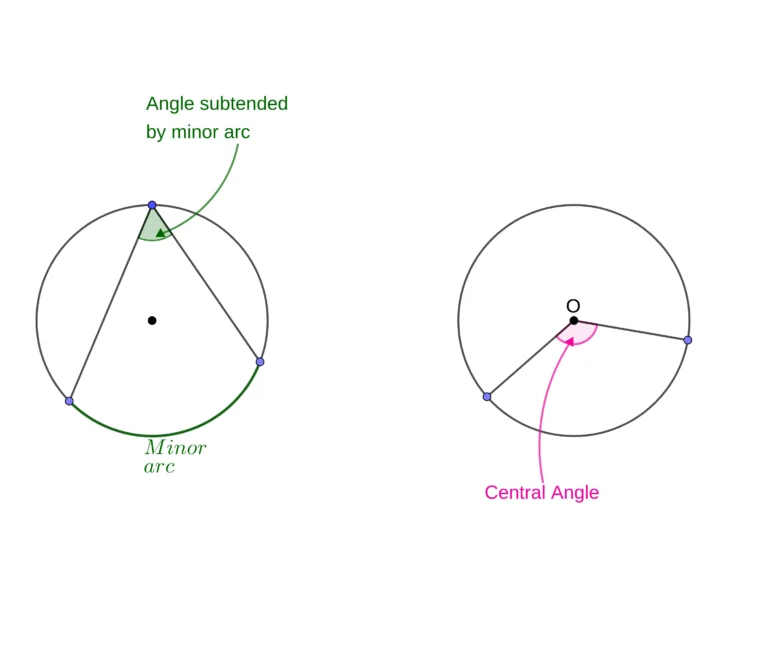
A chord is a line inside a circle that touches two points of the circumference. Depending on how the chord separates the circle, two segments, and arcs will be formed, one major and one minor.

Furthermore, there are two types of angles you can find in circle theorems: the subtended angle, and the central angle. The subtended angle is formed when two chords meet at a point on the circumference. The central angle is self-explanatory, forming at the center of the circle from two radii.
Circle Theorems
Circle Theorems describe various relationships between angles, and lengths that can be seen in various geometric constructions of circles.
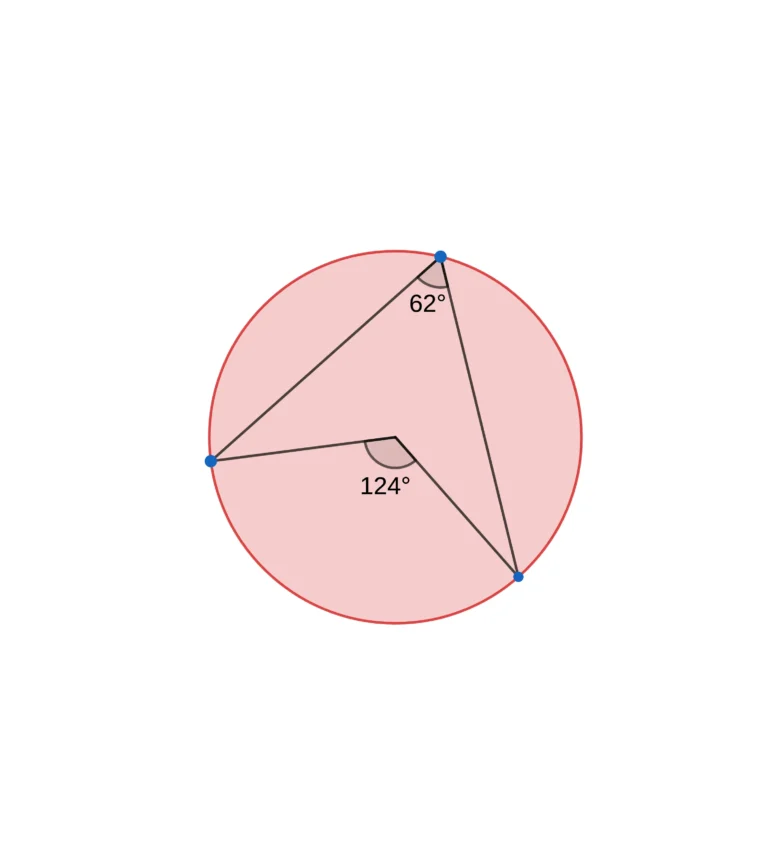
1. Central angle and subtended angle
The angle formed by an arc at the center (central angle) is twice the size of the angle formed by the same arc on the circumference (subtended angle).
2. Angles in a Semi-Circle
This theorem states that an angle in a semicircle is always 90 degrees or a right angle. Another way to understand this is that the angle formed by the diameter at any point on the circumference is a right angle.
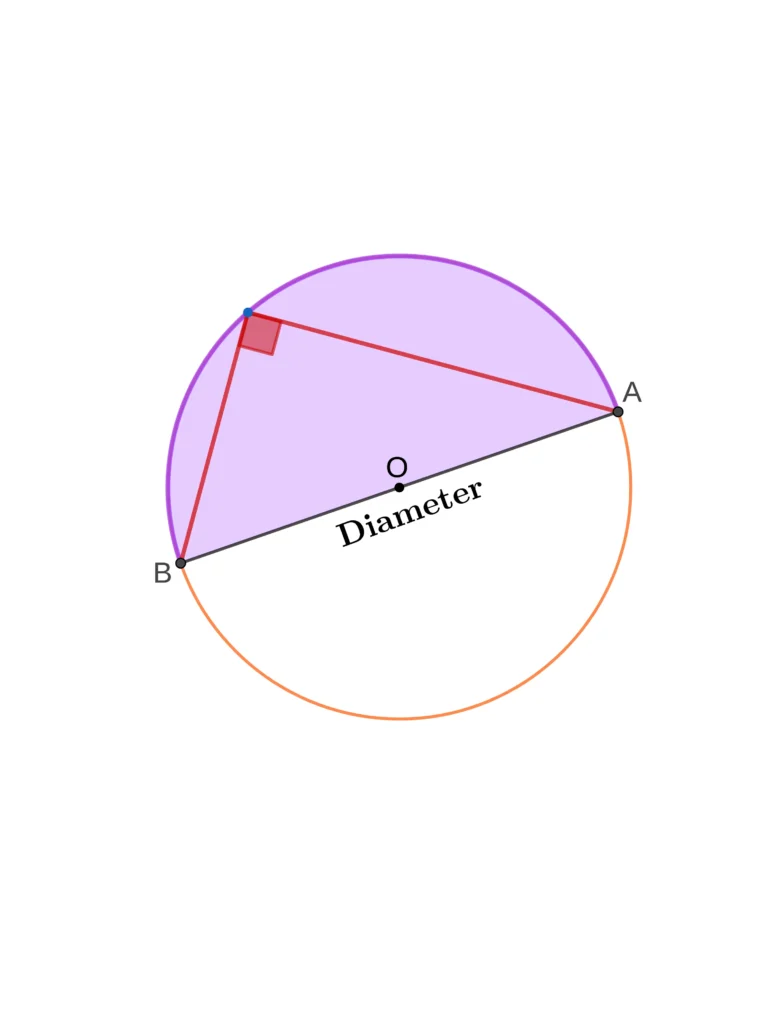
This can be seen as a special case of Theorem #1, where the arc considered is a semi-circular arc. Since the central angle subtended by a semi-circular arc is 180 degrees, by Theorem #1, the angle at the circumference must be half of it, which is 90 degrees.
3. Angles in The Same Segment
In a circle, angles formed by the same arc in a segment share equal measures. In other words, if two angles are subtended by the same arc, they are of equal size.

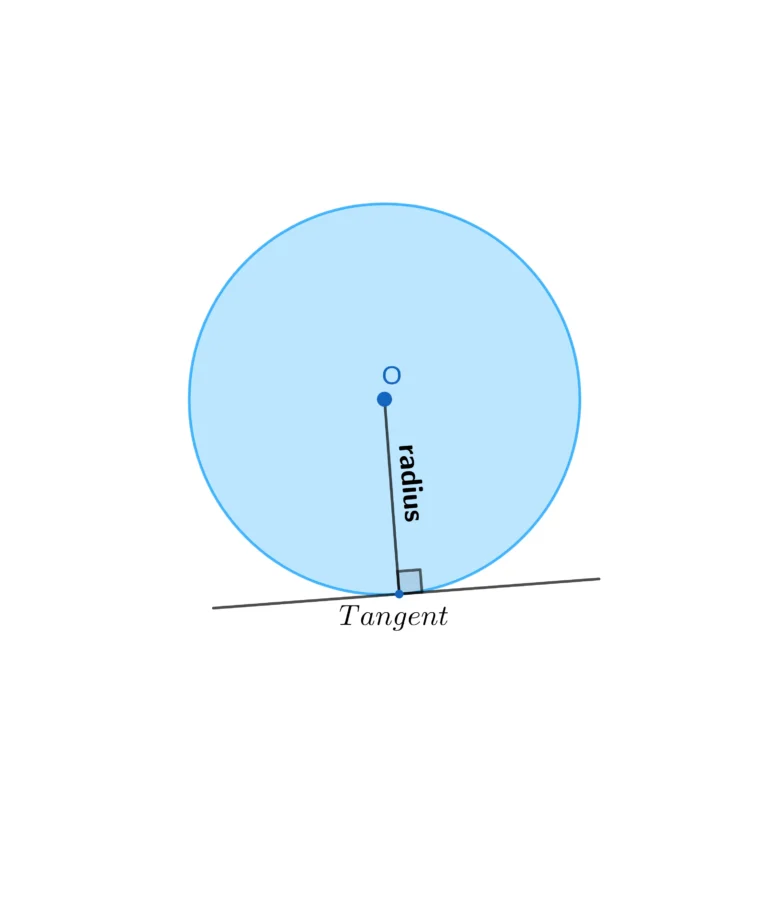
4. Tangent and Radius
A tangent is a line touching the circle at one point. It forms a right angle to the radius. The radius is perpendicular to a tangent to a circle, making a 90-degree angle. This theorem aids in comprehending how tangents and radii relate to one another.
5. Cyclic Quadrilateral
A cyclic quadrilateral is a four-sided polygon whose vertices all lie on the circumference of a circle. One of the key theorems related to cyclic quadrilaterals states that the sum of opposite angles in a cyclic quadrilateral is always equal to 180 degrees. This theorem has various applications in geometry, including in the analysis of geometric shapes and problem-solving.
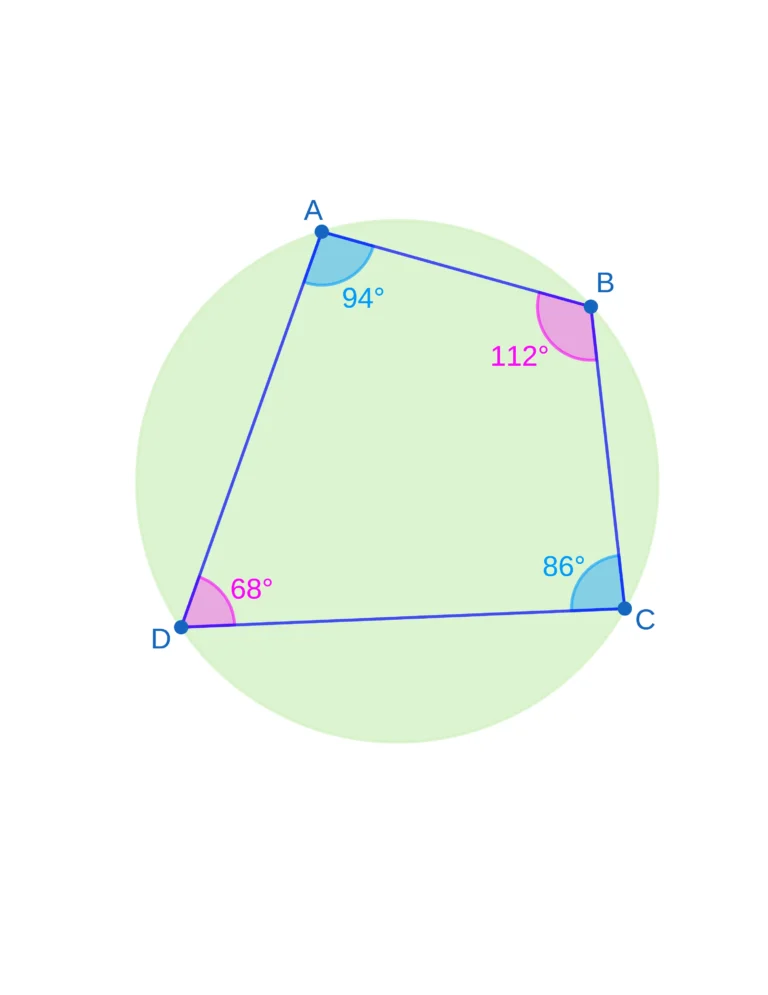
6. Intersecting chords
When two chords intersect within a circle, they create several angles and segments. One important theorem related to intersecting chords is that the product of the lengths of the segments formed by the chords is equal. This theorem is useful in various geometric problems, particularly those involving circles and their properties.
Conclusion
Circle theorems are like secret codes! Once you crack them, they can help you understand the magic of circles. These theorems show you how amazing and precise circles can be. By understanding tangents and angles in circles, the applications to solve real-world problems are limitless.